প্রোগ্রামিং কন্টেস্ট করার বেশ কিছু বড় সমস্যা আছে। তোমার কাছে ফুটবল খেলা বোরিং লাগবে আর টপকোডার বা কোডফোর্সেস এর স্কোরবোর্ড এক্সাইটিং লাগতে শুরু করবে। সবাই যখন ওয়ার্ল্ড কাপ নিয়ে মাতামাতি করা শুরু করবে তখন তুমি মাতামাতি করবে ওয়ার্ল্ড ফাইনালস নিয়ে। তোমার পাশ দিয়ে সানি, সিদকী বা সতেজ ভাই হেঁটে চলে গেলে তুমি বিষ্ফোরিত চোখে নিজেকে বিশ্বাস করানোর চেষ্টা করবে যে তোমার পাশ দিয়ে এই মাত্র আসলেই একটা রেড কোডার হেঁটে গেলো! কি ভয়াবহ ব্যাপার! প্রথমবার ডেট করতে গেলে তোমার মনে হবে এরচে’ টপকোডারে চ্যালেঞ্জ করতে গেলে তোমার বুক আরেকটু বেশি ধুবধুব করতো।
তারপর প্রোগ্রামিং কন্টেস্টকে যখন কেও হেয় করতে চাবে তোমার মাথায় রক্ত চড়ে যাবে। যেভাবে শেকসপিয়ারকে নিয়ে অশিক্ষিতরা হাসাহাসি করলে সিরিয়াস সাহিত্যের ছাত্রের মেজাজ গরম হয়ে যায়, কিংবা কেও একটা ডাইহার্ড হেভি মেটাল ফ্যানকে ‘হেভি মেটাল তো শুধুই নয়েজ’ টাইপের মহান বাণী দিলে তার মেজাজ যেভাবে খিঁচড়ায় সেরকম। কিন্তু তারপরও আমরা খুব একটা প্রতিবাদ করি না আর ভালোবাসি যা কিছু আমরা ভালোবাসি।
কারণ নিজে নিজে অনেক চিন্তাভাবনা করে একটা প্রবলেমের সমাধানে পৌছানোর একটা অন্য ধরণের সুখ আছে। অনেক সময় দিয়ে খেটেখুটে একটু একটু করে নিজেকে বুদ্ধিমান থেকে বুদ্ধিমানতর এবং চমৎকার থেকে চমৎকারতর প্রোগ্রামার হতে দেখার আনন্দ ঠিক বাদ্য বাজিয়ে দুনিয়াকে জানানোর মতো আনন্দ না। টপকোডারের চ্যালেঞ্জ ফেইজে পৃথিবীর সবচে’ সেরা প্রোগ্রামারের সলুশনে ভুল বের করে তুমি যদি একটা বিকট রণহুংকার ছাড়ো সেটার অ্যাপরেশিয়েটও হয়তো খুব বেশি মানুষ করবে না। তোমার বাবা হয়তো কানে ধরে তোমাকে বাসা থেকে বের করে দিবে। কিন্তু তাতে কি?
তারপরও আমরা ভালোবাসি যা কিছু আমরা ভালোবাসি।
প্রোগ্রামিং কন্টেস্ট করার জন্য সবার কিছু ন্যূনতম সংখ্যাতত্ত্ব জানা প্রয়োজন। এই জ্ঞানগুলো খুব বেসিক। কিন্তু তারপরও খুব গুরুত্বপূর্ণ। এই লেখাটায় পুরোটাই সেরকম টপিকগুলো নিয়ে, যেটুকু একদম না জানলেই নয়।
১ মৌলিক সংখ্যা
একটা সংখ্যা $n$ কে আমরা মৌলিক সংখ্যা বলে ডাকতে পারি যদি সংখ্যাটাকে শুধু $1$ আর $n$ দিয়ে নি:শেষে ভাগ করা যায়।
যেমন ধরো $5$ একটা মৌলিক সংখ্যা কারণ আমরা $5$ কে শুধু $1$ আর $5$ দিয়ে ভাগ করতে পারি কোন রকম ভাগশেষ না রেখে। আর কোন সংখ্যা দিয়ে $5$ কে ভাগ করা সম্ভব নয়। কিন্তু $6$ কি একটা মৌলিক সংখ্যা? উমম… নাহ! $6$ কে দেখো আমরা ভাগ করতে পারি $1, 2, 3$ আর $6$ দিয়ে। তো সংজ্ঞা অনুযায়ী $6$ মৌলিক সংখ্যা নয়। $1$ কে আমরা মৌলিক সংখ্যা হিসেবে বিবেচনা করি না।
যে কোন সংখ্যাকে কিছু মৌলিক সংখ্যার গুণফল হিসেবে ইউনিকভাবে প্রকাশ করা যায়। যেমন ধরো, $8 = 2^{3}$। কিংবা, $120 = 2^{3} \times 3 \times 5 $। আবার, $36 = 2^{2} \times 3^{2}$। তুমি যতই চেষ্টা করো না কেন $8, 120$ বা $36$ কে অন্য কোন মৌলিক সংখ্যার সেটের গুণফল হিসেবে প্রকাশ করতে পারবে না। এভাবে চিন্তা করতে গেলে একেকটা সংখ্যাকে যদি আমরা একেকটা দেয়াল হিসেবে ভাবি, মৌলিক সংখ্যাগুলো হচ্ছে তাদের একেকটা ইট। বাকি সব সংখ্যাগুলো মৌলিক সংখ্যার উপর ভিত্তি করে বানানো।
মৌলিক সংখ্যাকে ইংরেজিতে প্রাইম নাম্বার (prime number) বলে। আমরা এখন থেকে মৌলিক সংখ্যাকে প্রাইম নাম্বার ডাকবো।
১.১ প্রাইমালিটি টেস্টিং
একটা সংখ্যা $n$ প্রাইম কিনা সেটা বের করার জন্য সহজ একটা উপায় হচ্ছে আমরা সেটাকে $2$ থেকে $n-1$ সবগুলো সংখ্যা দিয়ে ভাগ করে দেখতে পারি যে সেটা কোনটা দিয়ে বিভাজ্য হয় কিনা। যদি সেটা বিভাজ্য না হয় (মানে নি:শেষে ভাগ করা যদি না যায়) শুধু তাহলেই সেটা মৌলিক সংখ্যা।
bool isPrime(int n) {
if (n < 2) return false;
for (int i = 2; i < n; i++) {
if (n % i == 0) {
return false;
}
}
return true;
}এভাবে চেক করার টাইম কম্প্লেক্সিটি হচ্ছে $\mathcal{O}(n)$। যেমন ধরো $1000000007$ প্রাইম কিনা সেটা চেক করার জন্য আমাদের রাফলি $1000000007-2 = 1000000005$ টা নাম্বার চেক করা লাগবে। আমরা এই টাইম কম্প্লেক্সিটিটাকে $\mathcal{O}(\sqrt{n})$ এ নামিয়ে আনতে পারি এটা খেয়াল করে যে, যদি সংখ্যাটা প্রাইম না হয় তাহলে আমরা $n$ কে দুটো সংখ্যার গুণফল হিসেবে লিখতে পারি।
এখন আমরা কন্ট্রাডিকশন (proof by contradiction) ব্যবহার করে প্রমাণ করতে পারি যে $a$ আর $b$ এর একটা সংখ্যা $\sqrt{n}$ এর থেকে ছোট বা সমান হবে। যদি আমরা যা ভাবছি তা সত্যি না হয়, তার মানে $a$ আর $b$ দুটোই $\sqrt{n}$ এর চেয়ে বড় হবে। কিন্তু যদি তা হয় তাহলে
কিন্তু সেটা তো হতে পারে না, তাই না? কারণ আমরা তো জানিই $a \times b = n$। তার মনে $a$ আর $b$ দুটোরই $\sqrt{n}$ এর চেয়ে বড় হওয়া সম্ভব না। সুতরাং তাদের একটা সংখ্যার $\sqrt{n}$ এর সমান বা ছোট হতেই হবে।
তার মানে আমাদের আসলে শুধু শুধু $n-1$ পর্যন্ত চেক করার আসলে দরকার নাই। আমরা $\sqrt{n}$ পর্যন্ত চেক করলেই পারি, কারণ $n$ যদি মৌলিক না হয় আমাদের প্রমাণ অনুযায়ী তার একটা ডিভিজর $\sqrt{n}$ এর মধ্যে থাকবে।
#include <cmath>
using namespace std;
bool isPrime(int n) {
if (n < 2) return false;
for (int i = 2; i <= sqrt(n) + 1; i++) {
if (n % i == 0) {
return false;
}
}
return true;
}কিন্তু এভাবে চেক করার একটা বড় সমস্যা হচ্ছে আমরা ডাবল প্রেসিশন নাম্বার (double precision number) কে ইন্টেজার (integer) এর সাথে তুলনা করছি। যেটা সবসময় যেভাবে তুমি আশা করছো সেভাবে হয়তো কাজ করবে না প্রেসিশন এরর এর জন্য (মিখাল ফরিশেক এর এই লেখাটা পড়ে দেখতে পারো আর জানতে চাইলে)।
আমরা সেজন্য সেটাকে এভাবে লিখি প্রেসিশন এরর এড়াবার জন্য।
bool isPrime(int n) {
if (n < 2) return false;
for (long long i = 2; i * i <= n; i++) {
if (n % i == 0) {
return false;
}
}
return true;
}তো এখন আমাদের $1000000007$ প্রাইম কিনা চেক করার জন্য মাত্র $31621$ টা নাম্বার দিয়ে চেক করলেই হবে। যেটা $1000000005$ থেকে অনেক অনেক ছোট একটা সংখ্যা।
প্রাইমালিটি টেস্টিং এর জন্য কিছু নন-ডিটারমিনিস্টিক অ্যালগরিদম আছে যেগুলো প্রোবালিস্টিক কিছু মেথড ব্যবহার করে প্রাইমালিটি টেস্ট করে। তুমি যদি সেগুলো নিয়ে পড়তে চাও অজয় সোমানির এই লেখাটা পড়তে পারো।
জাভার লাইব্রেরিতে একটা নন-ডিটারমিনিস্টিক অ্যালগরিদম লেখা আছে। আমার মনে হয় এইটুকু জানা ভালো।
import java.math.BigInteger;
public class PrimeTester {
public static boolean isPrime(int n) {
BigInteger number = new BigInteger(n + "");
return number.isProbablePrime(10);
}
public static void main(String[] args) {
System.out.println(isPrime(13));
}
}শুধু এটা মাথায় রেখো যে যদি isProbablePrime(certainity) রিটার্ন করে false তাহলে অবশ্যই সেটা প্রাইম না। কিন্তু যদি সেটা true রিটার্ন করে, তাহলে সেটা মৌলিক হতেও পারে নাও হতে পারে (এ কারণেই এটার নাম isProbablePrime) এবং সেক্ষেত্রে সেটা ভুল হবার প্রোবাবিলিটি $\frac{1}{2^{certainity}}$ এর মতো। যেমন আমার প্রোগ্রামটায় isPrime ভুল উত্তর দেবার প্রোবালিটি হচ্ছে $\frac{1}{2^{10}} \approx 0.098\%$। কিন্তু তুমি certainity এর মান যত বাড়াবো প্রোগ্রামটা প্রসেস করতে সমানুপাতে তত বেশি সময় লাগবে। জাভা ডকে উঁকি মারতে পারো আরো জানতে চাইলে।
১.২ এরাটস্থ্যানিজের সিভ
আমাদের এখনকার জ্ঞান দিয়ে আমরা যদি $n$ পর্যন্ত সবগুলো মৌলিক সংখ্যা বের করতে চাই, আমরা হয়তো এরকম একটা কোড লিখবো (আমি পুরো কোড আর সবগুলো হেডার ইচ্ছা করে লিখিনি - শুধু দরকারি অংশে মনোযোগ দেয়ার জন্য)।
#include <vector>
using namespace std;
vector<int> getPrimes(int n) {
vector<int> primes;
for (int i = 2; i <= n; i++) {
if (isPrime(i)) {
primes.push_back(i);
}
}
return primes;
}এই ইম্প্লিমেন্টেশনটার টাইম কম্প্লেক্সিটি হচ্ছে $\mathcal{O}(n \sqrt{n})$। আমরা এটাকে আরো ফাস্ট করতে পারি এরাটস্থ্যানিজের সিভ (Sieve of Eratosthenes) ব্যবহার করে, যেটার টাইম কম্প্লেক্সিটি হচ্ছে $\mathcal{O}(n \log(\log(n)))$। আমি তোমাকে এখন যেই অ্যালগরিদমটা শেখাবো সেটা দুই হাজার বছর পুরনো! মানে আমার বাবার বাবার বাবার বাবার বাবার … ৩০তম বাবার সময়ও মানুষ এই অ্যালগরিদমটা জানতো!
এরাটস্থ্যানিজের সিভ খুব সহজ একটা অ্যালগরিদম। আমি $n$ পর্যন্ত সবগুলো সংখ্যা লিখবো। তারপর একটা একটা করে সংখ্যা নিবো ছোট থেকে বড় অর্ডারে, যদি সেটা অলরেডি কাটা না হয় তাহলে ওটার সবগুলো মাল্টিপলকে কেটে ফেলবো। যেমন ধরো যদি আমরা $2$ পাই আমরা $4, 6, 8, 10, 12, 14, 16, \dots, 2i$ কে কেটে ফেলবো। কারণ $2$ এদের সবাইকেই তো নি:শেষে ভাগ করতে পারে, সুতরাং এদের কারোই প্রাইম হবার ক্ষমতা নাই।
এখন দেখো, আমরা যদি ছোট থেকে বড়তে যেতে যেতে এমন একটা সংখ্যা পাই যেটাকে এখনো কাটা হয় নাই, তাহলে তার মানে দাঁড়াচ্ছে আমরা এমন কোন সংখ্যা খুঁজে পাইনি যেটা ওই সংখ্যাটার চেয়ে ছোট এবং ওকে নি:শেষে ভাগ করতে পারে। তার মানে সেটা একটা প্রাইম নাম্বার!
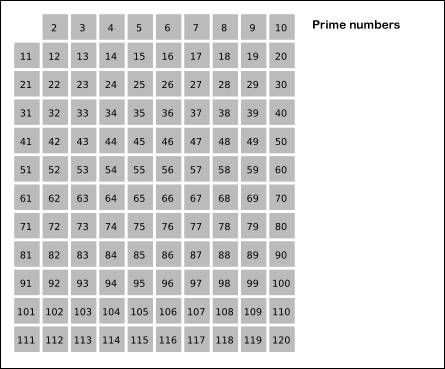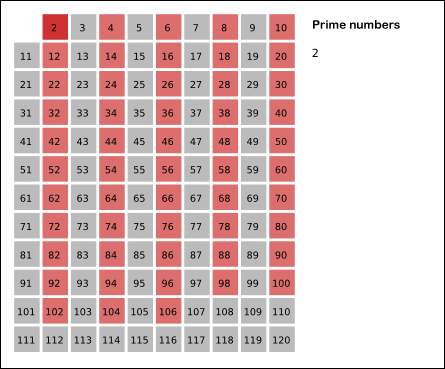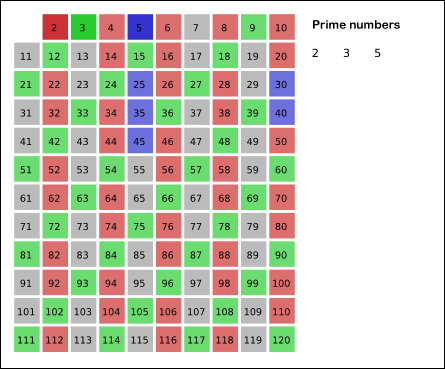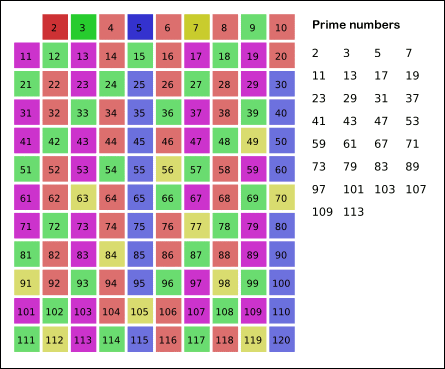
১.২.১ সাধারণ ইম্প্লিমেন্টেশন
#define M 1000000
bool marked[M];
void sieve(int n) {
for (int i = 2; i < n; i++) {
if (marked[i] == false) { // i is a prime
for (int j = i + i; j <= n; j += i) {
marked[j] = true;
}
}
}
}এই অংশটুকু সব কম্পোজিট নাম্বারগুলোকে মার্ক করে রাখবে এরাটস্থ্যানিজের অ্যালগরিদম অনুযায়ী । তো শুধু প্রাইম নাম্বারগুলো false হয়ে থাকবে marked অ্যারেতে।
আমরা আমাদের isPrime নতুন করে লিখতে পারি এভাবে।
bool isPrime(int n) {
if (n < 2) return false;
return marked[n] == false;
}দ্যাখো, sieve এর প্রথম লুপটা কিন্তু $n$ পর্যন্ত চালানো প্রয়োজন নেই। মনে আছে, আমরা প্রমাণ করেছিলাম প্রতিটা সংখ্যার একটা ডিভিজর থাকবে যেটা $\sqrt{n}$ সমান অথবা ছোট হবে? তো কোন সংখ্যা যদি প্রাইম না হয় তাহলে $\sqrt{n}$ সমান বা ছোট একটা সংখ্যা সেটাকে এমনিই মার্ক করবে। সেজন্য আমরা প্রথম লুপটা $\sqrt{n}$ চালালেই পারি। একই ব্যাপারটা ভেতরের লুপের জন্যও সত্যি। কেও যদি মার্ক করার হয় সেটা $\sqrt{n}$ এর মধ্যেই মার্কড হবে। তো আমরা $2i$ থেকে শুরু না করে $i^{2}$ থেকে শুরু করতে পারি।
#define M 1000000
bool marked[M];
void sieve(int n) {
for (int i = 2; i * i <= n; i++) {
if (marked[i] == false) { // i is a prime
for (int j = i * i; j <= n; j += i) {
marked[j] = true;
}
}
}
}আবার খেয়াল করো আমরা বারবার $2$ এর মাল্টিপলদের মার্ক করছি। যেমন ধরো, যখন $3$ এর মাল্টিপলদের মার্ক করছি তখন আমরা আসলে মার্ক করছি $6,9,12,15,18, … 3i$। যাদের অর্ধেক হচ্ছে $2$ এর মাল্টিপল। একই কথা বাকি সব প্রাইম নাম্বারদের জন্য সত্য। আমরা সেটা এড়াতে পারি শুধু অড মাল্টিপলগুলোকে মার্ক করে।
#define M 1000000
bool marked[M];
bool isPrime(int n) {
if (n < 2) return false;
if (n == 2) return true;
if (n % 2 == 0) return false;
return marked[n] == false;
}
void sieve(int n) {
for (int i = 3; i * i <= n; i += 2) {
if (marked[i] == false) { // i is a prime
for (int j = i * i; j <= n; j += i + i) {
marked[j] = true;
}
}
}
}১.২.২ মেমরি এফিশিয়েন্ট ইম্প্লিমেন্টেশন
আমাদের ইম্প্লিমেন্টেশনে আমরা কোন নাম্বার মার্কড কিনা বোঝার জন্য বুলিয়ান অ্যারে রাখছি, তাই না? একটা bool অবজেক্টের সাইজ হচ্ছে $8$ বিট। সাধারণত একটা বুলিয়ান ডাটা টাইপ মেশিনের addressable memory এর সবচে’ ছোট ইউনিট এর সমান জায়গা নেয়। যেমন আমার মেশিনে সেটা হচ্ছে এক বাইট। আর এক বাইট মানে হচ্ছে $8$ বিট। প্রতিটা বিট হচ্ছে একটা $0$ অথবা $1$। আমরা যদি কোনভাবে প্রতিটা বিটকে আলাদা আলাদা ব্যবহার করতে পারি সেটা মার্কড না আনমার্কড এটুকু ডাটা রাখার জন্য তাহলে আমাদের মেমরি ইউসেজ $8$ গুণ কমে যাবে। আর তারপর যদি আমরা সব জোড় সংখ্যাকে উপেক্ষা করি, তাহলে সেটা সবমিলে আমাদের মেমরি ইউসেজ $16$ গুণ কমিয়ে দেবে। একই সাথে বিট অপারেশনগুলো অনেক দ্রুত কাজ করে। সেটাও একটা প্লাস।
শুধু সমস্যা হচ্ছে সেটা করার জন্য তোমাকে বিট ম্যানিপুলেশন জানতে হবে (কিভাবে একটা নির্দিষ্ট বিটকে $0$ অথবা $1$ করবো বা ওটার ভ্যালু রিড করবো) আর কোডটা আরেকটু কম্প্লিকেটেড হবে। এখানে আমরা int ব্যবহার করছি যেটা হচ্ছে $32$ বিট। কিন্তু আমরা বারবার $64$ দিয়ে ভাগ করছি কারণ আমরা $2$ মাল্টিপলদের হিসেবে ধরছি না।
#define M 100000000
int marked[M/64 + 2];
#define on(x) (marked[x/64] & (1<<((x%64)/2)))
#define mark(x) marked[x/64] |= (1<<((x%64)/2))
void sieve(int n) {
for (int i = 3; i * i < n; i += 2) {
if (!on(i)) {
for (int j = i * i; j <= n; j += i + i) {
mark(j);
}
}
}
}
bool isPrime(int num) {
return num > 1 && (num == 2 || ((num & 1) && !on(num)));
}বিট ম্যানিপুলেশন নিয়ে জানতে পড়তে পারো ব্রুস মেরির এই লেখাটা।
১.৩ সেগমেন্টেড সিভ
যদি কখনো এরকম হয় যে প্রবলেমটা সলভ করার জন্য তোমার সবগুলো মৌলিক সংখ্যা বের করতে হবে $a=10000000000$ আর $b=10000100000$ এর মধ্যে তখন এটা দেখে ভয় পেয়ে ফিট হয়ে যেও না। এরকম প্রবলেমের জন্য যদি আমরা পুরো সিভটা চালাই আর $1$ থেকে $b$ পর্যন্ত সব প্রাইম বের করার চেষ্টা করি সেটা মেমরি আর সময়ের নিদারুণ অপচয় হবে।
আমরা যেটা করবো সেটা হচ্ছে আমরা প্রথমে $\sqrt{b} \approx 110000 $ পর্যন্ত সবগুলো প্রাইম বের করে নেবো। তারপর সেই প্রাইমগুলো দিয়ে সিভ চালাবো শুধু $[a, b]$ এই রেঞ্জের মাত্র $b-a+1$ টা সংখ্যার উপর।
তুমি যদি প্রোগ্রামারদের মতো করে ভাবো, তোমার প্রথম প্রশ্ন হওয়া উচিত ‘কেন সেটা কাজ করবে?’। ভালো প্রশ্ন, এটা কাজ করবে কারণ $b$ এর ছোট বা সমান কোন সংখ্যা যদি প্রাইম না হয় তার অবশ্যই একটা প্রাইম ডিভিজর থাকবে $[2,\sqrt{b}]$ এর মধ্যে। তো আমরা যখন সিভ চালাবো সেই প্রাইমগুলো কম্পোজিট নাম্বারগুলোকে মার্ক করবে।
তোমার দ্বিতীয় প্রশ্ন হওয়া উচিত, সিভ যে চালাবো, কোন সংখ্যা থেকে শুরু করবো সিভ চালানো?
এই প্রশ্নের উত্তর খোঁজার ভার আমি তোমার মস্তিষ্কের উপর ছেড়ে দিলাম। যেহেতু তুমি এই লেখাটা এতদূর পড়ে ফেলেছো, আমি বিশ্বাস করি যে তুমি বেশ মোটিভেটেড আর বুদ্ধিমান একটা মানুষ এবং তোমার পক্ষে নিজে নিজে এই উত্তরটা খুঁজে বের করা সম্ভব।
১.৪ অ্যাটকিনের সিভ
সিভের জন্য আরেকটা খুব ফাস্ট অ্যালগরিদম হচ্ছে অ্যাটকিনের সিভ (Sieve of Atkin)। অ্যাটকিন একটু কম্প্লিকেটেড এরাটস্থ্যানিজের চেয়ে কিন্তু এই বেঞ্চমার্কিং অনুযায়ী প্রথম দশ বিলিয়ন সংখ্যার ($n = 10^{10}$) জন্য আনঅপ্টিমাইজড এরাটস্থ্যানিজের $151$ সেকেন্ড লাগে যেখানে অ্যাটকিনের লাগে $36$ সেকেন্ড। কিন্তু $n$ এরপর বাড়াতে থাকরে দেখা যায় অ্যাটকিন স্লো পারফর্ম করতে শুরু করে এরাটস্থ্যানিজের তুলনায়।
আমি কখনো আমার কন্টেস্ট ক্যারিয়ারে অ্যাটকিনের সিভ ইম্প্লিমেন্ট করিনি। হয়তো তোমারও কখনো জিনিসটা প্রয়োজন হবে না। কিন্তু তারপরও অ্যাটকিনের সিভের নাম অন্তত জানা উচিত।
২ ডিভিজর কাউন্ট
২.১ সাধারণ অ্যালগরিদম
কোন সংখ্যা $n$ এর কয়টা ডিভিজর আছে সেটা বের করার জন্য আমরা $1$ থেকে $n$ পর্যন্ত লুপ চালাতে পারি।
int countDivisor(int n) {
int divisor = 0;
for (int i = 1; i <= n; i++) {
if (n % i == 0) {
divisor++;
}
}
return divisor;
}এটার টাইম কম্প্লেক্সিটি $\mathcal{O}(n)$। আমরা সেটাকে $\mathcal{O}(\sqrt{n})$ এ নামাতে পারি এটা খেয়াল করে যে যদি $n = a \times b$ আর তাদের একটা ডিভিজর যদি $\sqrt{n}$ এর ছোট হয়, অন্যটা অবশ্যই $\sqrt{n}$ এর বড় হবে (হিন্ট: কন্ট্রাডিকশন দিয়ে প্রমাণ করা সম্ভব)। সেজন্য $\sqrt{n}$ এর ছোট সবক’টা ডিভিজর এর জন্য আমরা divisor কে $1$ করে না বাড়িয়ে $2$ করে বাড়াতে পারি। শুধু যদি কোন ডিভিজর $\sqrt{n}$ সমান হয় তাহলে $1$ যোগ হবে।
যেমন ধরো, $18$ এর ডিভিজরগুলো হচ্ছে $1, 2, 3, 6, 9, 18$। $\sqrt{18}$ এর চেয়ে ছোট ডিভিজরগুলো হচ্ছে $1, 2, 3$ যেগুলোর প্রত্যেকটার জন্য আমরা আরেকটা ডিভিজর পাচ্ছি যেটা $\sqrt{18}$ এর চে’ বড় - $(1 \times 18) = 18, (2 \times 9) = 18, (3 \times 6) = 18$। আবার দেখো, $16$ এর ডিভিজরগুলো হচ্ছে $1, 2, 4, 8, 16$। যেটা দাঁড়াচ্ছে $(1 \times 16) = 16, (2 \times 8) = 16, (4 \times 4) = 16$। আমরা $4$ কে একবার গুনছি।
int countDivisor(int n) {
int divisor = 0;
for (int i = 1; i * i <= n; i++) {
if (i * i == n) {
divisor += 1;
} else if (n % i == 0) {
divisor += 2;
}
}
return divisor;
}২.২ অপটিমাইজড অ্যালগরিদম
ডিভিজর কাউন্টের অন্য সলুশনটা হচ্ছে প্রাইম ফ্যাকটোরাইজেশন। আমরা প্রতিটা সংখ্যা $n$ কে একটা ইউনিক মৌলিক সংখ্যার সেটের গুণফল হিসেবে লিখতে পারি।
যেমন ধরো, $18 = 2^{1} \times 3^{2}$ বা $120 = 2^{3} \times 3^{1} \times 5^{1} $। এখানে $r$ হচ্ছে প্রাইম ফ্যাক্টর এর সংখ্যা আর $\prod$ মানে হচ্ছে গুণফল। যেমন ধরো,
$18$ এর ডিভিজরগুলো হচ্ছে
একইভাবে $36$ এর ডিভিজরগুলো হচ্ছে
প্যাটার্নটা হচ্ছে প্রতিটা প্রাইম ফ্যাক্টর $P_{i}^{a_i}$ এর জন্য আমাদের হাতে $a_i+1$ টা আলাদা আলাদা অপশন আছে। যেমন শেষ উদাহরণটায় দেখো $2^{2}$ এর জন্য আমদের অপশন ছিলো তিনটা - $2^{0}, 2^{1}, 2^{2}$ । তো যদি সংখ্যাটা $18 = 2^{1} \times 3^{2}$ হয় আমাদের সবমিলে অপশন $2 \times 3 = 6$টা। আবার $36 = 2^{2} \times 3^{2}$ এর জন্য সেটা $3 \times 3 = 9$টা। যদি $n$ এর ডিভিজর কাউন্টকে আমরা $\sigma_0(n)$ দিয়ে প্রকাশ করি তাহলে -
#include <vector>
using namespace std;
vector<int> primes; // we'll preload primes once at the beginning
int countDivisor(int n) {
int divisor = 1;
for (int i = 0; i < primes.size(); i++) {
if (n % primes[i] == 0) {
int cnt = 1;
while (n % primes[i] == 0) {
n /= primes[i];
cnt++;
}
divisor *= cnt;
}
}
return divisor;
}আচ্ছা, এখানেও কি $\sqrt{n}$ টাইপের একটা অপটিমাইজেশন করা যায়? হুমম? বলতে পারো এই অ্যালগরিদমটার কম্প্লেক্সিটি কত হবে?
৩ GCD
GCD হচ্ছে Greatest Common Divisor। বাংলায় আমরা এটাকে বলি গ.সা.গু - গরিষ্ঠ সাধারণ গুণনীয়ক। যদি $gcd(a,b) = x$ হয় তাহলে $x$ হচ্ছে সবচে’ বড় সংখ্যা যেটা $a$ আর $b$ দুটাকেই নি:শেষে ভাগ করতে পারে।
#include <algorithm>
using namespace std;
int gcd(int a, int b) {
int ans = 1;
for (int i = 1; i <= min(a, b); i++) {
if (a % i == 0 && b % i == 0) {
ans = i;
}
}
return ans;
}কিন্তু GCD বের করার ভীষণ সুন্দর একটা হাজার বছর পুরনো অ্যালগরিদম আছে। আমরা $a$ আর $b$ এর GCD যদি বের করতে চাই আমরা এটাকে একটা $a \times b$ গ্রিড হিসেবে কল্পনা করি। আমরা খুঁজছি সবচে’ বড় সংখ্যা $x$ কে যাতে $x \times x$ সাইজের টাইলস দিয়ে আমরা এই পুরো গ্রিডটা ঢেকে দিতে পারি। স্কয়ার সাইজের টাইলস দিয়ে পুরো গ্রিডটা ঢাকতে চাইলে $x$ কে অবশ্যই একইসাথে $a$ আর $b$ এর ডিভিজর হতে হবে। একই সাথে যেহেতু $x$ সবচে’ বড় স্কয়ার সাইজ পুরো গ্রিড ঢাকার জন্য, সুতরাং এটা হচ্ছে তাদের GCD।

আমরা কি $a$ আর $b$ এর মধ্যে যেটা ছোট সেই সাইজের স্কয়ার দিয়ে গ্রিডটাকে কাভার করার করার চেষ্টা করি। যদি দেখি কাভার করা সম্ভব হচ্ছে না তাহলে যেই আয়তক্ষেত্রটা এখনো কাভার করা হয়নি সেটার সবচে’ ছোট পাশটা নিয়ে সেই সাইজের স্কয়ার দিয়ে বাকিটা কাভার করার চেষ্টা করি। এখানে রিমেইন্ডার নিলে আমরা সেই ছোট পাশটুকু পাবো যেটুকু আমরা কাভার করতে পারছি না। যেই সাইজের জন্য পুরো গ্রিডটাকে কাভার করা সম্ভব হবে, সেটাই হচ্ছে আমাদের GCD।
int gcd(int a, int b) { // assuming a >= b
while (true) {
int remainder = a % b;
if (remainder == 0) {
return b;
}
a = b; // a takes the bigger side
b = remainder; // b takes the smaller side
}
}এই অ্যালগরিদমটাকে রিকার্সিভলি লেখা যায় এভাবে -
int gcd(int a, int b) {
if(b == 0)
return a;
else
return gcd(b, a % b);
}আরেকটু ছোট করে এভাবেও লেখা যায় -
int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}আরেকটু ছোট করতে চাইলে তুমি এভাবেও লিখতে পারো। তবে এটা শুধু GNU এর কম্পাইলারে কাজ করবে।
int gcd = __gcd(a, b);৪ LCM
LCM হচ্ছে Least Common Multiple। বাংলায়, ল.সা.গু - লঘিষ্ঠ সাধারণ গুণিতক। যদি $lcm(a,b) = x$ হয় তাহলে $x$ হচ্ছে সবচে’ ছোট সংখ্যা যেটা $a$ আর $b$ দুটারই মাল্টিপল।
int lcm(int a, int b) {
for (int i = 1; ; i++) {
if (i % a == 0 && i % b == 0) {
return i;
}
}
}আরেকটা সহজ উপায় আছে LCM বের করার -
int lcm(int a, int b) {
return a * b / gcd(a, b);
}কিন্তু এভাবে লিখলে ওভারফ্লো হওয়ার একটা চান্স থাকে। মানে ধরো যেই সংখ্যাটা আমরা পাবো সেটা হয়তো int এর লিমিটে আঁটবে না। সেটা এড়ানোর জন্য আমরা এভাবে লিখতে পারি।
int lcm(int a, int b) {
return (a / gcd(a, b)) * b;
}এই অ্যালগরিদমটা নিয়ে আরো পড়তে পারো উইকিপিডিয়ায়।
৫ অয়লারের টশিয়েন্ট ফাংশন
টোশিয়েন্ট ফাংশনকে $\varphi(n)$ দিয়ে প্রকাশ করা হয়। $\varphi(n) = x$ যদি হয় তার মানে হচ্ছে $1$ থেকে $n$ পর্যন্ত $x$ টা সংখ্যা আছে যাদের সাথে $n$ এর GCD হচ্ছে $1$। যদি $gcd(a,b) = 1$ হয় আমরা বলি $a$ আর $b$ কো-প্রাইম (co-prime)।
যেমন ধরো $n = 9$ এর জন্য $gcd(9, 3) = gcd(9, 6) = 3$ আর $gcd(9, 9) = 9$ আর বাকি ছটা সংখ্যার জন্য
সেজন্য, $\varphi(9) = 6$।
অয়লারের প্রোডাক্ট ফরমুলা অনুযায়ী টোশিয়েন্ট এর মান এভাবে বের করা যায় -
এখানে $p$ হচ্ছে মৌলিক সংখ্যা আর $p|n$ মানে হচ্ছে সেইসব মৌলিক সংখ্যা যারা $n$ কে নি:শেষে ভাগ করতে পারে। যেমন ধরো যখন আমরা লিখি $a|b$, এর মানে হচ্ছে $a$ নি:শেষে ভাগ করতে পারে $b$ কে। মানে, $a$ হচ্ছে $b$ এর ডিভিজর।
যেমন ধরো,
যেহেতু, $120 = 2^{3} \times 3^{1} \times 5^{1} $
৫.১ সাধারণ ইম্প্লিমেন্টেশন
vector<int> primes; // we'll preload primes once at the beginning
int phi(int n) {
int ret = n;
for (int i = 0; i < primes.size(); i++) {
if (n % primes[i] == 0) {
ret -= ret / primes[i];
}
}
return ret;
}এটাকে একটু অপটিমাইজ করা যায় নিচের কোডটার মতো করে লিখে। তোমার কি যথেষ্ট মনের জোর আছে নিজে নিজে বোঝার চেষ্টা করার নিচের কোডটা কেন কাজ করছে?
int phi (int n) {
int ret = n;
for (int i = 2; i * i <= n; i++) {
if (n % i == 0) {
while (n % i == 0) {
n /= i;
}
ret -= ret / i;
}
}
// this case will happen if n is a prime number
// in that case we won't find any prime that divides n
// that's less or equal to sqrt(n)
if (n > 1) ret -= ret / n;
return ret;
}তোমার ভয় কাটানোর জন্য আমি এখানে একটা কার্টুন জুড়ে দিলাম।
৫.২ অপটিমাইজড ইম্প্লিমেন্টেশন
টোশিয়েন্ট ফাংশন আরেকভাবে লেখা যায়। তবে এভাবে লেখা তখনই কাজে লাগে যখন আমরা আগে থেকে জানি আমাদের অনেকবার টোশিয়েন্ট ফাংশনকে কল করা লাগবে। সেক্ষেত্রে আমরা টোশিয়েন্টকে সিভের মতো করে লিখতে পারি। মানে ছোট থেকে বড় যখনই একটা প্রাইম নাম্বার পাবো আমরা করবো ওই প্রাইম নাম্বারটার সব মাল্টিপলগুলোর টোশিয়েন্ট ভ্যালু আপডেট করবো।
#define M 1000005
int phi[M];
void calculatePhi() {
for (int i = 1; i < M; i++) {
phi[i] = i;
}
for (int p = 2; p < M; p++) {
if (phi[p] == p) { // p is a prime
for (int k = p; k < M; k += p) {
phi[k] -= phi[k] / p;
}
}
}
}৬ এক্সটেন্ডেড ইউক্লিড
এক্সটেন্ডেড ইউক্লিডিয়ান অ্যালগরিদম যেকোন $a$ আর $b$ এর জন্য $x$ ও $y$ খুঁজে বের করে যেন
এক্সটেন্ডেড ইউক্লিডের রিকার্সিভ অ্যালগরিদমটার বেইস কেস হচ্ছে যখন $b=0$ হয়। সেক্ষেত্রে আমরা $(1,0)$ রিটার্ন করবো। অন্যক্ষেত্রে আমরা $(b, a \bmod b)$ কে কল করে যেই রেজাল্টটা পাবো $(x,y)$ সেটা ব্যবহার করে $(y, x - y * (a/b) )$ রিটার্ন করবো।
তোমার মাথায় যদি প্রশ্ন জাগে, ‘কেন এটা কাজ করবে?’ - তাহলে আমি খুব খুশি হবো। তুমি ঠিক প্রশ্ন জিজ্ঞেস করছো। প্রুফটা তুমি পাবে এখানে।
typedef pair<int, int> pii;
#define x first
#define y second
pii extendedEuclid(int a, int b) { // returns x, y | ax + by = gcd(a,b)
if(b == 0) return pii(1, 0);
else {
pii d = extendedEuclid(b, a % b);
return pii(d.y, d.x - d.y * (a / b));
}
} ৭ মাল্টিপ্লিকেটিভ মডুলার ইনভার্স এবং কিছু মডুলার অ্যারিথমেটিক
প্রোগ্রামিং কন্টেস্টে সব সময় ঠিক এক্সাক্ট রেজাল্ট চাওয়া হয় না। তোমাকে বরং একটা মডুলো ভ্যালু আউটপুট দিতে বলা হতে পারে। যেমন ধরো, প্রশ্নটা এরকম হতে পারে - $1, 2, 3, 4, 5, 6, 7, 8$ - এই কয়েকটা ডিজিট প্রতিটা যদি $9$ ৰার করে দেয়া থাকে তাহলে তাদের দিয়ে যতগুলো ইউনিক সংখ্যা বানানো সম্ভব তাদের সবার যোগফল বের করো। এখন এই যোগফলটা যেহেতু অনেক বড় হতে পারে যেটা long long এ আটবে না। সেজন্য তোমাকে বলা হতে পারে $ answer \bmod 10000007$ আউটপুট দিতে ( $ a \bmod b$ মানে হচ্ছে $a$ কে যদি আমি $b$ দিয়ে ভাগ করি তাহলে যেই ভাগশেষ থাকবে সেটা)।
মডুলার অ্যারিথমেটিকে যোগ, বিয়োগ আর গুণ করা বেশ সহজ। মানে যদি
হয়, তাহলে যোগ, বিয়োগ আর গুণের জন্য নিচের আইডেন্টিটিগুলো সত্যি হবে।
যেমন ধরো, কেও যদি আমাকে $(1+2+3+ \dots + n) \bmod {11}$ বের করতে বলে আমি তখন এভাবে লিখতে পারি।
int findSum(int n) {
int sum = 0;
for (int i = 1; i <= n; i++) {
sum += i;
sum %= 11;
}
return sum;
}আবার যদি $(1 \times 2 \times 3 \times \dots \times n) \bmod {11}$ বের করতে হয় তখন এভাবে লেখা যায়।
int findFactorial(int n) {
int factorial = 1;
for (int i = 1; i <= n; i++) {
factorial *= i;
factorial %= 11;
}
return factorial;
}কিন্তু ভাগ করতে গেলে একটা বিশাল ঝামেলা লেগে যায়, সেটা আর এত সহজ ভাবে কাজ করে না। তো ধরো যদি আমরা কোন কিছুকে $b$ দিয়ে ভাগ করতে চাই তাহলে সরাসরি না ভাগ করে আমরা $b^{-1}$ দিয়ে গুণ করি। এই $b^{-1}$ কে আমরা বলি $b$ এর মডুলার ইনভার্স। এদের জন্য নিচের আইডেন্টিটিটা সত্যি
যেমন ধরো যদি $b = 3 $ আর $n = 11 $ হয় তাহলে, $3^{-1} $ হবে $4$ , কারণ $ 3 \times 4 = 12 \equiv 1 \pmod {11}$।
মডুলার ইনভার্স বের করা যায় এক্সটেন্ডেড ইউক্লিড ব্যবহার করে। এক্সটেন্ডেড ইউক্লিড এরকম একটা আইডিন্টিটির জন্য $(x,y)$ খুঁজে বের করে $(a,b)$ এর জন্য।
এখন মডুলার ইনভার্স হচ্ছে অনেকটা এরকম - যেখানে $x$ হচ্ছে মডুলার ইনভার্স, যেটাকে আমরা খুঁজছি
তারমানে হচ্ছে আমরা যদি extendedEuclid কে কল করি $(a, n)$ দিয়ে আমরা $a$ এর মডুলার ইনভার্স পাবো। অবশ্যই $gcd(a,n) = 1$ হতে হবে। তা না হলে মাল্টিপ্লিকেটিভ মডুলার ইনভার্স থাকা সম্ভব না।
int modularInverse(int a, int n) {
pii ret = extendedEuclid(a, n);
return ((ret.x % n) + n) % n;
}আরেকটা সহজ উপায় আছো মডুলার ইনভার্স বের করার ফার্মার লিটল থিওরেম (Fermat’s Little Theorem) আর ফাস্ট এক্সপোনেনসিয়েশন (Fast Exponentiation) ব্যবহার করে। তবে সেটা একটু সীমাবদ্ধ, শুধু কাজ করে যখন $n$ প্রাইম নাম্বার হয় তখন।
৮ উপসংহার
এই আর্টিকেলটা পড়াটা অনেকটা কুস্তি শিখতে গিয়ে একটা নরম সোফায় বসে পেস্ট্রি আর ফ্যানের বাতাস খেতে খেতে পালোয়ানের কাছ থেকে কুস্তির গল্প-কিচ্ছা শোনার মতো। হয়তো এই গল্প-কিচ্ছা তোমাকে প্রয়োজনীয় জ্ঞান দিবে, ইন্সপায়ার করবে, ট্রিক শেখাবে - কিন্তু তুমি যদি সাহস করে কুস্তির ময়দানের ময়লা কাদায় লুঙ্গি কোঁচ মেরে না নামো আর কয়েকটা কোমড়ভাঙ্গা আছাড় না খাও তাহলে এই সব জ্ঞান, পেস্ট্রি আর গল্প (বা লুঙ্গি) কোন কিছুই কাজে আসবে না।
সেজন্য জর্জ পোলজা বলতো, প্রবলেম সলভিং শেখা হচ্ছে সাঁতার কাটা শেখার মতো। আর প্রবলেম সলভিং শেখার একমাত্র উপায় হচ্ছে প্রবলেম সলভ করা।
আমি তোমাকে কিছু প্রবলেমের লিস্ট দিচ্ছি এখানে, কুস্তি করার জন্য। কিছু প্রবলেম অনেক কঠিন, তোমার বুকে অনেকটুকু সাহস একসাথে করতে হবে এরকম প্রবলেমের মুখোমুখি হবার জন্য। তুমি যতটুকু বুদ্ধিমান তোমাকে তার চে’ বুদ্ধিমান হবার চেষ্টা করতে হবে সেগুলো সলভ করতে। ক্রমাগত ব্যর্থতাকে পান্তাভাত ভাবতে হবে।
আমরা আসলে ঠিক এভাবেই বড় হই। আমাদের সীমাবদ্ধতার চোখ রাঙ্গানি উপেক্ষা করে সেটা অতিক্রম করার চেষ্টা করাটাই আমাদের আরো বড় করে। এবং আমাদের সামর্থ্য দেয় আরো কঠিন কিছু করার। তুমি যদি কখনো এভাবে চিন্তা করতে শুরু করো, তোমার কাছে সম্ভব আর অসম্ভব এর দেয়ালটা অদৃশ্য থেকে অদৃশ্যতর হতে শুরু করবে।
৮.১ রিলেটেড প্রবলেম
৮.২ রেফারেন্স
৮.৩ কৃতজ্ঞতা স্বীকার
মো: মাহবুবুল হাসানকে ধন্যবাদ তার মূল্যবান পরামর্শের জন্য (যেগুলো এই লেখাটাকে আরো স্ট্রাকচার্ড করতে সাহায্য করেছে) এবং একই সাথে কিছু গুরুত্বপূর্ণ টপিক যোগ করতে মনে করিয়ে দেবার জন্য। মেহেদী রহমানকে ধন্যবাদ আমার মডুলার ইনভার্সের কোডে ভুল বের করে দেবার জন্য এবং লেখাটাকে গাণিতিকভাবে রিগোরাস করতে সাহায্য করার জন্য। জাবির ইবনে কামালকে ধন্যবাদ ডিভিজর কাউন্টের কোডে ভুল সংশোধন করে দেবার জন্য। হাসনাইন হেইকেল জামি এবং শাফায়েত আশরাফকে ধন্যবাদ আমাকে রিলেটেড প্রবলেম খুঁজে দেবার জন্য। তোমাদের সাহায্য আর অনুপ্রেরণা ছাড়া এই বিশাল লেখাটা আমার পক্ষে লেখা সম্ভব হতো না।



