১ প্রবলেম
যখন আমারা কোন রিকারেন্স রিলেশনের n-তম পদ খুঁজে বের করার চেষ্টা করি এবং সেই রিকারেন্স ফাংশানের যদি প্যারামিটার একটা থাকে তাহলে সাধারণত লিনিয়ার সময় লাগে (মানে টাইম কম্প্লেক্সিটি হয় $\mathcal{O}(n)$)। এখানে আমরা এমন একটা অ্যালগোরিদম নিয়ে আলোচনা করবো যেটা রিকারেন্স রিলেশনের n-তম পদ খুঁজে বের করবে আরো কম কমপ্লেক্সিটিতে।
যেমন ধরো, ফিবোনাচি সিকোয়েন্স হচ্ছে এক ধরণের রিকারেন্স রিলেশন। সেখানে প্রথম দুটো ছাড়া প্রতিটি n-তম পদ হচ্ছে তার আগের দুটো পদের যোগফল।
আমরা একটা লুপ চালিয়ে ফিবোনাচি বের করতে পারি লিনিয়ার সময়ে।
long long fibonacci(int n) {
if(n < 2) return 1;
long long f[100];
f[1] = f[2] = 1;
for (int i = 3; i <= n; i++) {
f[i] = f[i-1] + f[i-2];
}
return f[n];
}কিন্তু এটা কি আরো কম টাইম কম্প্লেস্কিটিতে করা সম্ভব?
২ ম্যাট্রিক্সের গুণফল দিয়ে রিকারেন্স প্রকাশ
ফিবোনাচি রিকারেন্সটা ম্যাট্রিক্সের মাধ্যমে প্রকাশ করা সম্ভব। আমরা ফিবোনাচি সিকোয়েন্স এর রিকারেন্সটাকে এভাবে লিখতে পারি।
সব ধরণের লিনিয়ার রিকারেন্সকে আমরা আসলে ম্যাট্রিক্সের গুণফলের মাধ্যমে প্রকাশ করতে পারি। যেমন ধরো, এই রিকারেন্সটাকে
ম্যাট্রিক্স দিয়ে প্রকাশ করলে সেটা হবে এরকম
আমরা ফিবোনাচির রিকারেন্সটাকে আরেকটু সহজভাবে প্রকাশ করতে পারি এভাবে লিখে
৩ ফাস্ট এক্সপোনেনসিয়েশন
এর আগের অংশের ফিবোনাচির রিকারেন্সটাকে আমরা এভাবে লিখতে পারি
এখন ব্রুটফোর্স এর মাধ্যমে আমরা যদি এই আইডিয়াটা ইমপ্লিমেন্ট করে ম্যাট্রিক্স এর n-তম পাওয়ার বের করি এবং সেটাকে ইনিশিয়াল টার্ম এর সাথে গুন করি তাহলে আগের কমপ্লেক্সিটিই থেকে যায়। সেটা সলভ করার উপায় হচ্ছে ফাস্ট এক্সপোনেনসিয়েশন।
একটা ইন্টিজার k এর জন্য যদি আমরা k এর n-তম পাওয়ার খুঁজে বের করতে চাই, তাহলে আমরা কী করবো? খুব সোজাভাবে চিন্তা করলে তুমি বলে বসবে, “কী আর করবো, k কে n বার গুন করবো”। কিন্তু একটু লক্ষ্য করলে দেখা যায়,
আর এই পদ্ধতিতে পাওয়ার বের করলে, তার কমপ্লেক্সিটি মাত্র $\mathcal{O}(log n)$। যেমন নিচের উদাহরণটাতে আমরা $3^{10}$ বের করতে মাত্র $4$ টা অপারেশন লাগাচ্ছি, $10$ টার বদলে
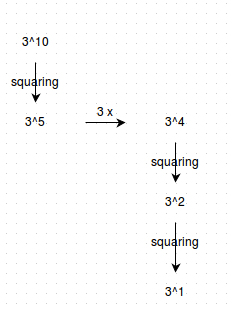
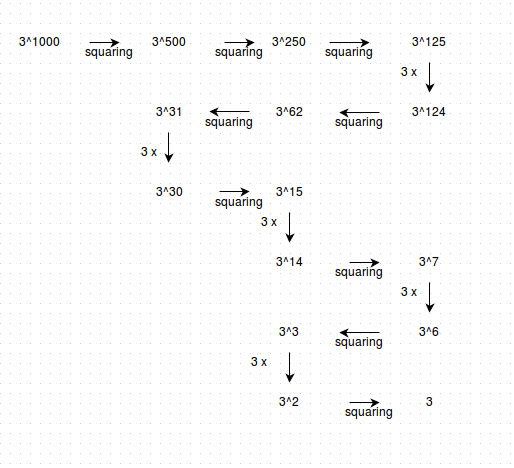
আরেকটা উদাহরণ দিলে হয়তো সহজ হবে বোঝা। ধরো, আমরা বের করতে চাই $3^{1000}$
// finding a^p
int power(int a, int p) {
if (p == 0) return 1;
if (p == 1) return a;
if (p % 2 == 1)
return a * power(a, p - 1);
int ret = power(a, p / 2);
return ret * ret;
}ম্যাট্রিক্সের জন্য সেটা এরকম হবে -
matrix power(matrix mat, int p) {
if (p == 0) return identity_matrix;
if (p == 1) return mat;
if (p % 2 == 1)
return multiply(mat, power(mat, p - 1));
matrix ret = power(mat, p / 2);
ret = multiply(ret, ret);
return ret;
}যদি ম্যাট্রিক্সটা $k \times k$ হয়, এভাবে n-তম পদ খুঁজে বের করার টাইম কম্প্লেক্সিটি হবে $\mathcal{O}(k^{3}\times log(n))$)।
৪ জেনারালাইজেশন
যদি লিনিয়ার রিকারেন্সটাকে এরকম হয়
তাহলে সেটাকে ম্যাট্রিক্সে দিয়ে প্রকাশ করলে সেটা হবে -
সহজেই বোঝা যাচ্ছে যে, প্রথম রো তে আমাদের সবগুলো কো-এফিশিয়েন্ট রাখতে হবে কারণ ডানপাশে আমাদের প্রথম এলিমেন্টটা হচ্ছে g(n)। যেহেতু আমরা g(n-1) এর মান রাখতে চাই ডানের ম্যাট্রিক্স এর দ্বিতীয় row-তে, তাই x(2, 1) এর মান অবশ্যই 1 হতে হবে। একইভাবে x(3, 2), x(4, 3), x(5, 4), …, x(k, k-1) = 1 করতে হবে, বাকি মানগুলো অবশ্যই 0 হতে হবে।
আর প্রথম k টা এলিমেন্ট যদি b(1), b(2), …, b(k) হয় তাহলে জেনারালাইজড রিকারেন্সটা হবে এরকম -
৫ ইম্প্লিমেন্টেশন
৫.১ সহজ প্রবলেম
ম্যাট্রিক্স এক্সপোনেসিয়েশন বোঝার জন্য একটা সহজ প্রবলেম হচ্ছে “Yet Another Number Sequence” (সাদরুল হাবিব চৌধুরী)। আমাকে নিচের রিকারেন্স দেয়া আছে। আমাকে n-তম পদের শেষ m টা ডিজিট প্রিন্ট করতে হবে লিডিং জিরো ছাড়া।
যদি প্রথম পদটা 1 থেকে শুরু হতো আর প্রথম দুটো ভ্যালু 1 হতো আমরা ফিবোনাচির রিকারেন্সটা ব্যবহার করতে পারতাম।
এই প্রবলেমটার জন্য শুধু মূল ম্যাট্রিক্সের ওপর পাওয়ারটা পাল্টাবে আর ডানের ম্যাট্রিক্সটা পাল্টাবে। বাকি জিনিসগুলো একই থাকবে।
#include <iostream>
#include <cassert>
using namespace std;
struct matrix {
int v[5][5];
int row, col; // number of row and column
};
int mod = 10000;
// multiplies two matrices and returns the result
matrix multiply(matrix a, matrix b) {
assert(a.col == b.row);
matrix r;
r.row = a.row;
r.col = b.col;
for (int i = 0; i < r.row; i++) {
for (int j = 0; j < r.col; j++) {
int sum = 0;
for (int k = 0; k < a.col; k++) {
sum += a.v[i][k] * b.v[k][j];
sum %= mod;
}
r.v[i][j] = sum;
}
}
return r;
}
// returns mat^p
matrix power(matrix mat, int p) {
assert(p >= 1);
if (p == 1) return mat;
if (p % 2 == 1)
return multiply(mat, power(mat, p - 1));
matrix ret = power(mat, p / 2);
ret = multiply(ret, ret);
return ret;
}
int main() {
int tcase;
int a, b, n, m;
cin >> tcase;
while (tcase--) {
// input routine
cin >> a >> b >> n >> m;
// preparing the matrix
matrix mat;
mat.row = mat.col = 2;
mat.v[0][0] = mat.v[0][1] = mat.v[1][0] = 1;
mat.v[1][1] = 0;
// preparing mod value
mod = 1;
for (int i = 0; i < m; i++) mod *= 10;
a %= mod, b %= mod;
if (n < 3) {
if (n == 0) cout << a << endl;
if (n == 1) cout << b << endl;
if (n == 2) cout << (a+b) % mod << endl;
} else {
mat = power(mat, n - 1);
int ans = b * mat.v[0][0] + a * mat.v[0][1];
ans %= mod;
cout << ans << endl;
}
}
return 0;
}৫.১ কঠিন প্রবলেম
“How many Knight Placing?” (আব্দুল্লাহ আল মাহমুদ, ২০০৬) এ আমাদেরকে $6 \times N$ সাইজের একটা দাবার বোর্ড দেয়া আছে (মানে $6$ টা রো আর $N$ টা কলাম)। এখানে $N$ যেকোন সংখ্যা হতে পারে $1$ এবং $1000000000$ এর মধ্যে। প্রতিটা কলামে $2$ টা করে ঘোড়া (Knight) বসাতে হবে এমনভাবে যাতে কেউ কাউকে অ্যাটাক না করে।

$N$ এর জন্য বের করতে হবে কতভাবে আমরা বোর্ডটায় $2N$ টা ঘোড়া বসাতে পারি যাতে প্রতি কলামে দুইটা করে ঘোড়া থাকে আর কেউ কাওকে যাতে অ্যাটাক না করে। যেহেতু প্রকৃত উত্তরটা অনেক বড় একটা সংখ্যা হবে, আমরা answer modulo 10007 প্রিন্ট করবো।
এই প্রবলেমটা আসলে একটা গ্রাফ থিওরী প্রবলেম। যদি আমাদেরকে একটা গ্রাফ দেয়া থাকে যার অ্যাডজাসেন্সি ম্যাট্রিক্স হচ্ছে $A$, যেখানে $i$ আর $j$ এর মধ্যে এজ থাকলে $A(i,j) = 1$ আর এজ না থাকলে $A(i,j) = 0$ তাহলে যদি জিজ্ঞেস করা এই গ্রাফটাতে কতগুলো ইউনিক $n$ লেন্থের পথ থাকা সম্ভব, সেটার উত্তর হবে $A^{n}$ ম্যাট্রিক্সের সবগুলো এলিমেন্টের যোগফল। কেন?
এই প্রবলেমটাতে ব্যাকট্র্যাকিং চালিয়ে অল পসিবল কম্বিনেশনের ভ্যালিড দুই কলামকে আমরা একটা করে নোড ধরবো। তারপর যেই নোডগুলো পাশাপাশি বসানো যায় (একটা কলাম ওভারল্যাপ করে) তাদের মধ্যে এজ বসিয়ে অ্যাডজাসেন্সি ম্যাট্রিক্স বানাবো। তারপর সেটার পাওয়ার রেইজ করবো $A^{N-2}$ এ। তারপর সেই ম্যাট্রিক্সটার সবগুলো এলিমেন্টের যোগফল নিলে সেটা হবে আমাদের উত্তর।
৬ অপটিমাইজেশন এবং অন্যন্য খুঁটিনাটি
কন্টেস্টের জন্য আরেকটি খুব প্রচলিত একটা রেকুয়ার্মেন্ট হলো answer মডিউলো একটি সংখ্যা। এর কারণ হলো, প্রকৃত answer অনেক বেশি বড় যা সহজে প্রকাশ করা যায় না। এই টেকনিকটা এই সিমুলেশনের জন্য বেশ ভাল কাজ করে, কারন এখানে শুধু যোগ (+) এবং গুন(*) অপারেশন করা হয়। প্রত্যেক বেসিক কমপিউটেশানের এর জন্য প্রতিবার রেজাল্ট মডিউলো m বের করতে হবে। অবশ্যই সতর্ক থাকতে হবে যাতে করে ওভারফ্লো না হয়, কারন, যদিও ম্যাট্রিক্স এর মান গুলো ছোট কিন্তু এক্সপোনেনসিয়েশন আলগোরিদম একসঙ্গে দুটি ম্যাট্রিক্স গুণ করে বড় মান তৈরী করতে পারে। খেয়াল রাখতে হবে যে ডাটাটাইপ তুমি ব্যবহার করছো তার ধারণ ক্ষমতা যেন $m \times m$ থেকে বড় হয়।
রিকার্শন ব্যবহার করার একটা সমস্যা হচ্ছে যদি ম্যাট্রিক্সের সাইজ খুব বড় হয় তাহলো সেটা স্ট্যাক ওভারফ্লো খেতে পারে। সেক্ষেত্রে আমরা বটম আপ অ্যাপরোচে হিসেব করতে পারি। সেটা আসলে দুই ভাবে করা যায়। আমরা যেভাবে ফাস্ট এক্সপোনেনসিয়েশন করছিলাম সেটাকে বটম আপ করে করা যায়। মানে আমরা একই কাজটাই করবো শুধু উল্টো দিক থেকে। সেক্ষেত্রে পাওয়ারের অংশটাতে কোডটা পাল্টে এরকম হবে -
string binary(int p) {
string ret = "";
while (p > 0) {
ret += (p % 2 == 0) ? "0" : "1";
p /= 2;
}
reverse(ret.begin(), ret.end());
return ret;
}
matrix power(matrix mat, int p) {
string bin = binary(p);
matrix ret = mat;
for (int i = 1; i < bin.size(); i++) {
ret = multiply(ret, ret);
if (bin[i] == '1') {
ret = multiply(ret, mat);
}
}
return ret;
}আরেকটা উপায় হচ্ছে আমরা প্রথমে ২ এর পাওয়ারগুলো স্টোর করে রাখতে পারি। তারপর সেই অনুযায়ী যেকোন একটা পাওয়ারের ভ্যালু বের করতে পারি।
যেমন ধরো,
তো এভাবে যেকোন সংখ্যার পাওয়ার আসলে বের করে ফেলা যায় পাওয়ারটার বাইনারী ভ্যালু দেখে।
যখন ম্যাট্রিক্স কে গুন করা হয়, তখন রেফারেন্স পাঠানো যায় multiply ফাংশনে, কল বাই ভ্যালু করার দরকার নাই, এতে করে, ফাংশন প্যারামিটারের ভ্যারিয়েবলে মান কপি করার সময়টুকু বেঁচে যায়।
void multiply(matrix &a, matrix &b) {
}আমরা আরেকটু অপটিমাইজ করতে পারি রেজাল্টটাকে রেফারেন্স হিসেবে পাঠিয়ে।
void multiply(matrix &a, matrix &b, matrix &res) {
//matrix res ; this is not necessary
}শুধু এই অপটিমাইজেশনটা করার সময় এই ধরণের ফাংশন কল কোর না।
multiply(ret, ret, ret);৭ প্রবলেম লিস্ট
৮ কৃতজ্ঞতা স্বীকার
এই লেখাটা লিখতে অনুপ্রাণিত করেছেন জানে আলম জান এবং ইংরেজি থেকে বাংলায় অনুবাদে সাহায্য করেছে রিমন মোস্তাফিজ।

